TLDR
(click to show/hide)
A funny historical incident where Pi = 3.2 was almost codified into Indiana State Law and some additional mathematical background
on the topic of geometric constructions in general for those that are interested.
You'll have to forgive me. I'm writing this article hastily on 3/15 to release as my belated Pi Day post. I was actually
searching for an intriguing math fact or some interesting proof to write about on the subject of Pi as I did with
Elementary Not Easy: The Irrationality of Pi a few years ago but nothing
struck me yesterday until, of course, as I was lying in bed last night. Scrolling through my phone just before sleeping, I saw this meme
on Reddit:
Reading into the story behind it a bit, I found it had just enough historical intrigue and a good enough proportion of geometry to talk about.
This was the article I wanted to write about and is now my new favorite math fact about Pi (aside from Buffon's Needle).
The Story of the Indiana Pi Bill
Centuries had it been unknown whether squaring the circle was possible with traditional
geometric construction (a compass and straightedge). But in 1882
Lindemann and Weierstrass had proven a theorem which, as a consequence, established that the transcendence of Pi which, as a further consequence, made
the ancient task impossible. The problem now determined, joined a group of other well known
impossible classic constructions of geometry. This did not stop
Edward J. Goodwin, a physician from Solitude, Indiana from believing he had a solution 15 years later in 1897. He had published on Goodwin's model circle
to the American Mathematical Monthly that in fact there was a solution to the "impossible" construction:
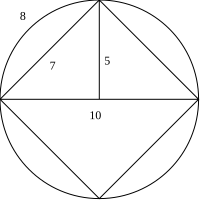
Goodwin's model circle (the proposed solution to squaring the circle with compass and straightedge)
As a gesture of goodwill, he wanted to contribute his finding as a gift to Education in the State of Indiana by codifing his model into law with
the ENGROSSED HOUSE BILL No. 246. Now, take a moment to yourself
reader, and see the immediate flaw with the model above. With the numbers provided, you can likely prove to yourself fairly quickly that π = 3.2 exactly. This
had likely slipped by the legislature since they may not have understood the "proof"
that was provided to them.
Luckily, on the day of the bill's proposal, Purdue University mathematics professor Clarence Waldo
happened to be present for an unrelated matter (seeking the annual appropriation for the Indiana Academy of Science). Noticing the Bill in the day's schedule along with the
impossibility of the result immediately, he discussed it with other senators before it was to be voted on. When it reached the Senate Floor, the senators Waldo had alerted got the
bill idefinitely postponed.
The incident reached the Chicago Tribune, Indianapolis News, and other publications which all poked fun.
On Non-Impossible Geometric Constructions
Geometric construction dates back to Ancient Greece
where mathematicians had first attempted ways to perform math algorithmically via geometry. The most basic of these included the following those to
do with points, lines, and circles which could be extended to more complex procedures for finding fractions of angles, n-sided regular polygons, etc:
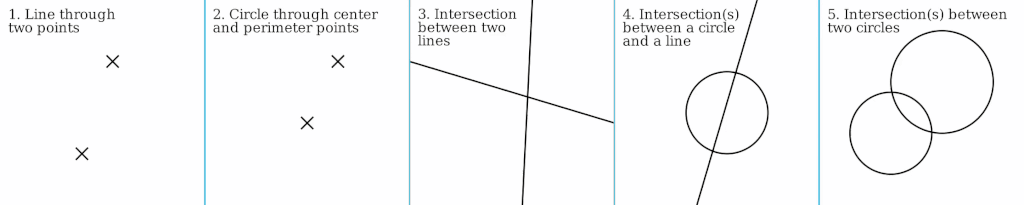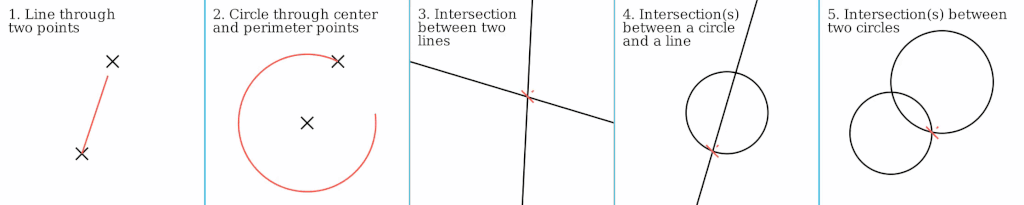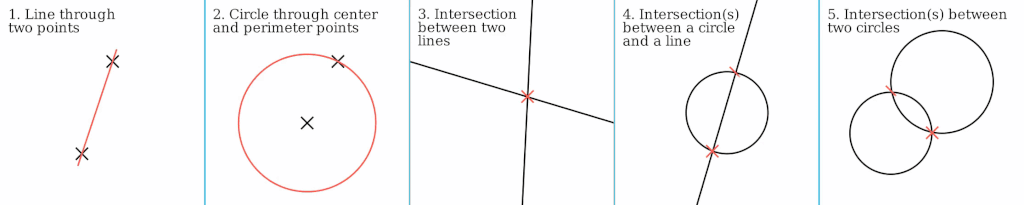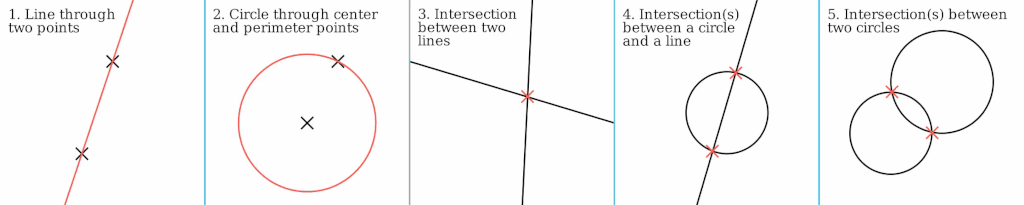
Basic geometric constructions with compass and straightedge
After centuries, progress stalled until Gauss discovered how to construct a Heptadecagon
and eventually Hilbert found a complete set of axioms for geometry describing the field
as an axiomatic algebra. I found this to be a pretty cool fact I did not know / think about before which can actually be fairly shortly stated:
Axiom System for Geometry:
-
Primitive Objects
-
Primitive Relations
- Betweenness (ternary relation on points)
- Lies on (Containment), three binary relations linking points and straight lines, points and planes, and straight lines and planes
- Congruence two binary relations linking line segments and linking angles
With the above alone, one can construct line segments, angles, triangles, polygons, and the rest of Euclidean solid geometry. Unfortunately
they do not fit neatly as a First-Order Theory, but a later set of axioms by
Tarksi (1926) can be represented as such.
I have not read this book on the topic,
but I imagine it would be quite interesting. Among its topics are Euclidean Constructions, variations of construction axioms, and paperfolding.
Conclusion
Geometric constructions are a cool field of math for both their rich history and their eventual linking to algebra by Hilbert.
Algebraic Geometry has since expanded well beyond these old problems.
As an eventual consequence somewhere between the two Pi was proven to be a transcendal number which made the Indiana Pi Bill all the funnier
both at the time, and still today.
Hope y'all enjoyed and happy Pi Day!