Samuel Perales

The Ping Pong Lemma

5 / 25 / 21

Next >

7 min read

TLDR (click to show/hide)

A brief introduction to abstract algebra, the ping-pong lemma (which lets you prove something about an infinitely large group with a finite amount of work), and how I made an algorithm utilizing it in my research in the Texas Experimental Geometry Lab (TXGL).

Today I'm going to talk about an interesting lemma in abstract algebra and how I used it in my research at the Texas Experimental Geometry Lab. Before we talk about the lemma, let's first establish some of the mathematical background we'll need to know.

Abstract algebra / algebraic structures is all about the study of groups, rings, fields, and the properties of these objects. A group $G$ is a set along with a binary operation $\cdot$ such that the following properties are satisfied:

Closure: For $a, b \in G$ , we have that $a \cdot b$ is in $G$
Associativity: For $a, b, c \in G$ , we have a $a \cdot (b \cdot c) = (a \cdot b) \cdot c$
Identity: There exists an $e \in G$ such that for any $a \in G$ , $e \cdot a = a \cdot e = a$
Inverses: For $a \in G$ , there is $a^{- 1} \in G$ such that $a \cdot a^{- 1} = e$

A group presentation is a collection of generators and relations such that $G = 〈 generators | relations ⟩$ . Perhaps this is best understood with a few examples:

$〈 a, b ⟩$ is the set of all multiples of $a$ and $b$ (such as $a^{k}$ for any integer $k$ or $a b a b^{- 2}$ etc.)
The integers with the addition operation can be written as $ℤ = 〈 1 ⟩$ since $1^{k}$ (which is to say $1$ added to itself $k$ times since the operation is addition) will generate all of the integers.
$〈 a | a^{3} = 1 ⟩$ is a group with the set of elements ${e, a, a^{2}}$ since we have the relation which dictates that $a^{3}$ must be the identity.

The group we will consider today is $S L_{2} (ℝ)$ which is the set of 2x2 real matrices with determinant 1 along with the operation of standard matrix multiplication. Once we have the concept of a group, we need to understand what a group action is. Essentially, a group action is a map which takes $G \times X$ to $X$ for some space $X$ and preserves the group operation (ie. $g (h x) = (g h) x$ ). The space we will primarily consider is the real projective line $ℝ P^{1}$ which is the set of equivalence classes of lines (often represented by a circle).

Now that we have some of the terminology we need, lets talk about the problem we want to solve. We call a group action faithful if each element of the group other than the identity acts nontrivially on the space $X$ , that is, there is no $g \in G$ such that $g x = x$ for all $x \in X$ . In general, it is very hard to show that a given group has a faithful action on a space. However, we do know that a certain type of group called a free group will always have a faithful action. Free groups are groups with no relations (ie. there are no elements formed by the generators which give us the identity). So, if we want an approach to the problem of determining if a group will have a faithful action on a space, we can attempt to show that the group is isomorphic (equivalent) to a free group.

This is where the ping pong lemma comes into play. Below we will state the lemma and see immediately how it will be useful in solving our problem.

Ping Pong Lemma: Suppose a and b are generators for a group G which acts on a space X. If:

$X$ has disjoint nonempty subsets $X_{a}$ and $X_{b}$

$a^{k} (X_{a})$ is contained in $X_{a}$ and $b^{k} (X_{b})$ is contained in $X_{b}$ for all nonzero $k$

then $G$ is isomorphic to a free group of rank 2.

Without the ping pong lemma, we would need to check an infinite number of conditions to see if a groups action is faithful (we would need to see that $g x \neq x$ for all $g$ and for all $x$ ). But here, we have a finite number of conditions to check to see that the group is free and therefore faithful. The research done in TXGL consisted of extending this lemma to $n$ generators in $S L_{2} (ℝ)$ and coming up with an algorithm to search for intervals which will satisfy these properties.

Avoiding diving too far into the details of the algorithm, I will talk about the basic procedure. The idea is that the since the eigenvectors of our generators are fixed points under the action of the generator in $ℝ P^{1}$ , we know that the intervals must include them. By creating epsilon intervals around these, we have initial intervals to start the search with. From here, we expand endpoints of the intervals, checking if they satisfy the necessary containment properties until we find them. There are different method for interval expansion we tried which are discussed on the TXGL project writeup.

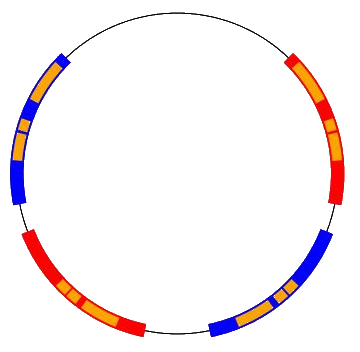
Here is an example of intervals in $ℝ P^{1}$ which satisfy the necessary containment properties to show that the respective group action is faithful:

There are a lot of details left out in this discussion so if you want to learn more of the math or more about the algorithm, check out these other resources:

TXGL Project Writeup (Ping Pong and Beyond)

Office Hours with a Geometric Group Theorist

Repository for TXGL Ping Pong

Personal Blog

The Ping Pong Lemma

5 / 25 / 21

Next >

7 min read

A brief introduction to abstract algebra, the ping-pong lemma (which lets you prove something about an infinitely large group with a finite amount of work), and how I made an algorithm utilizing it in my research in the Texas Experimental Geometry Lab (TXGL).

Today I'm going to talk about an interesting lemma in abstract algebra and how I used it in my research at the Texas Experimental Geometry Lab. Before we talk about the lemma, let's first establish some of the mathematical background we'll need to know.

Abstract algebra / algebraic structures is all about the study of groups, rings, fields, and the properties of these objects. A group $G$ is a set along with a binary operation $\cdot$ such that the following properties are satisfied:

Closure: For $a, b \in G$ , we have that $a \cdot b$ is in $G$

Associativity: For $a, b, c \in G$ , we have a $a \cdot (b \cdot c) = (a \cdot b) \cdot c$

Identity: There exists an $e \in G$ such that for any $a \in G$ , $e \cdot a = a \cdot e = a$

Inverses: For $a \in G$ , there is $a^{- 1} \in G$ such that $a \cdot a^{- 1} = e$

A group presentation is a collection of generators and relations such that $G = 〈 generators | relations ⟩$ . Perhaps this is best understood with a few examples:

$〈 a, b ⟩$ is the set of all multiples of $a$ and $b$ (such as $a^{k}$ for any integer $k$ or $a b a b^{- 2}$ etc.)

The integers with the addition operation can be written as $ℤ = 〈 1 ⟩$ since $1^{k}$ (which is to say $1$ added to itself $k$ times since the operation is addition) will generate all of the integers.

$〈 a | a^{3} = 1 ⟩$ is a group with the set of elements ${e, a, a^{2}}$ since we have the relation which dictates that $a^{3}$ must be the identity.

This is where the ping pong lemma comes into play. Below we will state the lemma and see immediately how it will be useful in solving our problem.

Here is an example of intervals in $ℝ P^{1}$ which satisfy the necessary containment properties to show that the respective group action is faithful:

There are a lot of details left out in this discussion so if you want to learn more of the math or more about the algorithm, check out these other resources:

TXGL Project Writeup (Ping Pong and Beyond)

Office Hours with a Geometric Group Theorist

Repository for TXGL Ping Pong

Samuel Perales

Personal Blog

The Ping Pong Lemma

5 / 25 / 21

Next >

7 min read

A brief introduction to abstract algebra, the ping-pong lemma (which lets you prove something about an infinitely large group with a finite amount of work), and how I made an algorithm utilizing it in my research in the Texas Experimental Geometry Lab (TXGL).

Today I'm going to talk about an interesting lemma in abstract algebra and how I used it in my research at the Texas Experimental Geometry Lab. Before we talk about the lemma, let's first establish some of the mathematical background we'll need to know.

Abstract algebra / algebraic structures is all about the study of groups, rings, fields, and the properties of these objects. A group G is a set along with a binary operation ⋅ such that the following properties are satisfied:

Closure: For a,b∈G, we have that a⋅b is in G

Associativity: For a,b,c∈G, we have a a⋅(b⋅c)=(a⋅b)⋅c

Identity: There exists an e∈G such that for any a∈G, e⋅a=a⋅e=a

Inverses: For a∈G, there is a−1∈G such that a⋅a−1=e

A group presentation is a collection of generators and relations such that G=〈generators|relations⟩. Perhaps this is best understood with a few examples:

〈a,b⟩ is the set of all multiples of a and b (such as ak for any integer k or abab−2 etc.)

The integers with the addition operation can be written as ℤ=〈1⟩ since 1k (which is to say 1 added to itself k times since the operation is addition) will generate all of the integers.

〈a|a3=1⟩ is a group with the set of elements {e,a,a2} since we have the relation which dictates that a3 must be the identity.

This is where the ping pong lemma comes into play. Below we will state the lemma and see immediately how it will be useful in solving our problem.

Ping Pong Lemma: Suppose a and b are generators for a group G which acts on a space X. If: X has disjoint nonempty subsets Xa and Xb ak(Xa) is contained in Xa and bk(Xb) is contained in Xb for all nonzero k then G is isomorphic to a free group of rank 2.

Here is an example of intervals in ℝP1 which satisfy the necessary containment properties to show that the respective group action is faithful:

There are a lot of details left out in this discussion so if you want to learn more of the math or more about the algorithm, check out these other resources: TXGL Project Writeup (Ping Pong and Beyond) Office Hours with a Geometric Group Theorist Repository for TXGL Ping Pong

Abstract algebra / algebraic structures is all about the study of groups, rings, fields, and the properties of these objects. A group $G$ is a set along with a binary operation $\cdot$ such that the following properties are satisfied:

Closure: For $a, b \in G$ , we have that $a \cdot b$ is in $G$

Associativity: For $a, b, c \in G$ , we have a $a \cdot (b \cdot c) = (a \cdot b) \cdot c$

Identity: There exists an $e \in G$ such that for any $a \in G$ , $e \cdot a = a \cdot e = a$

Inverses: For $a \in G$ , there is $a^{- 1} \in G$ such that $a \cdot a^{- 1} = e$

A group presentation is a collection of generators and relations such that $G = 〈 generators | relations ⟩$ . Perhaps this is best understood with a few examples:

$〈 a, b ⟩$ is the set of all multiples of $a$ and $b$ (such as $a^{k}$ for any integer $k$ or $a b a b^{- 2}$ etc.)

The integers with the addition operation can be written as $ℤ = 〈 1 ⟩$ since $1^{k}$ (which is to say $1$ added to itself $k$ times since the operation is addition) will generate all of the integers.

$〈 a | a^{3} = 1 ⟩$ is a group with the set of elements ${e, a, a^{2}}$ since we have the relation which dictates that $a^{3}$ must be the identity.

Here is an example of intervals in $ℝ P^{1}$ which satisfy the necessary containment properties to show that the respective group action is faithful:

There are a lot of details left out in this discussion so if you want to learn more of the math or more about the algorithm, check out these other resources:

TXGL Project Writeup (Ping Pong and Beyond)

Office Hours with a Geometric Group Theorist

Repository for TXGL Ping Pong