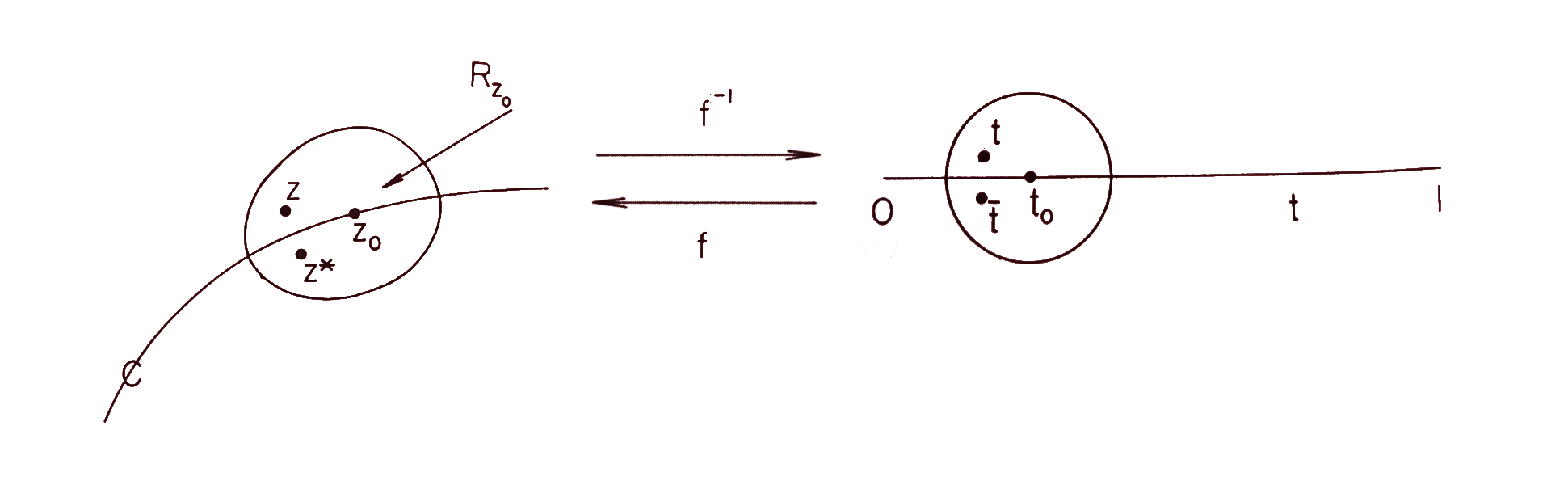Samuel Perales

Schwarzian Reflection

7 min read

TLDR (click to show/hide)

Mirrors are cool and relatively easy to represent mathematically, at least when they're flat... What happens if you want to represent a reflection across any shape other than a line/plane though? It turns out we can turn to some complex analysis with something called a Schwartz function which lets us find some explicit solutions for reflections across all sorts of interesting curves.

At some point, back in a geometry class in middle or high school, we all learned how to reflect points across lines. We just need to find the line perpendicular to the one we're wanting to reflect across passing through the point we want to reflect, and then get the point the same distance down the line on the other side.

This isn't terribly hard, but what does it look like to reflect a point across an arbitrary curve instead? What about closed shapes like ellipses? It seems clear that our reflected point should still be along the line orthogonal to the curve, but how far should it be reflected? How would we calculate this? Let's first remind ourselves of a bit a complex analysis before looking at the answer to these questions.

Background

• Conjugate Coordinates

  The complex plane is defined as $ℂ:=\{z=x+iy:x,y\in ℝ\}$. Each point $z=x+iy$ has a complex conjugate $\mathrm{z̄}=x-iy$ which is the reflection of $z$ across the real-axis.

• Regular Points

  For a curve given by $f(x,y)=0$, a point $p$ along the curve is called regular if $\frac{\partial f}{\partial x}{|}_p\ne 0$ and $\frac{\partial f}{\partial y}{|}_p\ne 0$ (that is, all of the non-critical points along the curve).

• Analytic Functions

  Functions which are complex-differentiable at all points in a region $R$ are called analytic / holomorphic where complex differentiability is defined in the same way as for real functions.

• Implicit Function Theorem

  The Implicit Function Theorem can take some time to explain on its own, but essentially, it tells us that if we have a smooth (differentiable) function, we can solve for either of its variables. Please look into the provided link if you want to learn more about why this works.

Schwarz Function for an Analytic Arc

Suppose we have an arc $C$ in the plane given by $F(x,y)=0$. We can rewrite this curve in conjugate coordinates as per the section above as $F(x,y)=F(\frac{z+\mathrm{z̄}}{2},\frac{z-\mathrm{z̄}}{2i})=g(z,\mathrm{z̄})=0$.

Now suppose that $g(z,\mathrm{z̄})$ is an analytic function. For a point $z_0$ on the curve $C$, if we have that $\frac{\partial g}{\partial \mathrm{z̄}}{|}_{z_0}\ne 0$, then we can solve for $\mathrm{z̄}$ uniquely using the Implicit Function Theorem to get $\mathrm{z̄}=S\left(z\right)$. The theorem tells us that $S\left(z\right)$ is regular and analytic in a neighborhood of $z_0$. If all points along $C$ are regular points (ie. they hold the property that their derivative with respect to $\mathrm{z̄}$ is nonzero), we can define $S\left(z\right)$ in an entire strip-like region around the curve.

This tells us that for any regular curve, we can find a unique function that maps points on the curve to their conjugate value. But how does $S$ act on points in the neighborhood surrounding our curve? We explore this in the next section.

Schwarzian Reflection

A curve $C$ given by:

$\{\begin{array}{l}x=f_1(t)\\ y=f_2(t)\end{array}$   where   $0\le t\le 1$ and $z\left(t\right)=f_1\left(t\right)+i{f}_2\left(t\right)=f\left(t\right)$

is a simple analytic arc if:

• only if $t_1=t_2$ (this is the simple part; the curve does not intersect itself)

• $f_1\left(t\right)$ and $f_2\left(t\right)$ are real analytic functions for $0\le t\le 1$

• $z^{\text{'}}\left(t\right)={f^{\text{'}}}_1\left(t\right)+i{f^{\text{'}}}_2\left(t\right)\ne 0$ for $0\le t\le 1$

For a point $t_0\in [0,1]$, the function $f\left(t\right)$ is analytic in some circle $|t-t_0|\le \lambda \left(t_0\right)$, and since $f$ has nonzero derivative as per our assumptions, it maps a sub-circle $|t-t_0|\le {\lambda }_1\le \lambda \left(t_0\right)$ one-to-one conformally onto a region $R_{z_0}$ containing $z_0=f\left(t_0\right)$. Therefore, any $z\in R_{z_0}$ is the image of a unique $t$.

Now, if we consider $z^{*}=f_1(\overline{t})+i{f}_2(\overline{t})$, we see that it is the Schwarz reflection of $z$ in $C$ where reflection is given by the sequence $z\to t\to \overline{t}\to z^{*}$ as depicted in the figure below.

We can relate $z^{*}$ back to the Schwarz function by noting that ${\mathrm{z̄}}^{*}=f_1(t)-i{f}_2(t)$ since $f_i$ are real-valued analytic functions and $f_i(\overline{t})=f_i\left(t\right)$. From there, we can deduce that:

$x=f_1(t)=\frac{z+{\mathrm{z̄}}^{*}}{2}$, $y=f_2(t)=\frac{z-{\mathrm{z̄}}^{*}}{2i}\to F(\frac{z+\mathrm{z̄}}{2},\frac{z-\mathrm{z̄}}{2i})=g(z,\mathrm{z̄})=0\to {\mathrm{z̄}}^{*}=S(z)\to z^{*}=S(z)$

So the Schwarzian reflection is the complex conjugate of the Schwarz function! With this exciting connection, we can finally move on to a more interactive example in the next section.

Example

The Schwarz function of a circle centered at $z_0$ with radius $r$ is given by $S(z)=\frac{r^2}{z-z_0}+{\mathrm{z̄}}_0$. For any set of points within a neighborhood of the circle, such as the parametrized ellipse below, we can pass them through the Schwarz function, take the complex conjugate, and get the reflected points in the circle.

Resources

• The Schwarz Function and Its Applications (Book by Philip J Davis)
• Implicit Function Theorem